Uncovering compositional structure in neural networks
Tom McCoy, Tal Linzen, Ewan Dunbar, Paul Smolensky
This page accompanies the paper found here. The code is available here.
Introduction: No duplication without representation
Neural networks are widely celebrated for their ability to handle complex tasks. However, they have another ability that might be even more impressive because it is more surprising: They can also solve tasks that they seem extremely ill-suited for.
Consider the task of copying a sequence of digits. Intuitively, this task seems to require compositional representations that indicate the sequence’s fillers (that is, which specific digits are in the sequence) and those fillers’ roles (that is, their positions). The standard way of writing a sequence is shorthand for such a filler-role representation:
4 , 3 , 7 , 9 , 6 = 4 : first + 3 : second + 7 : third + 9 : fourth + 6 : fifth
Neural networks do not appear to use any such representation of structure, so asking a neural network to perform a symbolic task might seem like using a Phillips screwdriver on a flathead screw. Nonetheless, the neural network below is able to perform the copying task very successfully:
This neural network has two components: the encoder, which encodes the sequence into a vector of continuous values (represented here as shades of blue); and the decoder, which generates the output sequence based on the vector encoding.
This network is not perfect—for example, it fails on most single-digit sequences—but it does perform extremely well, with over 99% accuracy on a held-out test set. The question, then, is this: How can neural networks use continuous vector representations to perform symbolic tasks that depend on compositional structure? In this project, we investigate the following hypothesis:
In the rest of this project description, we first discuss filler-role representations in more detail. Next, we investigate analogies as a preliminary source of evidence for filler/role representations in neural networks. Finally, we introduce a novel architecture, the Tensor Product Decomposition Network (TPDN) for decomposing learned vector representations into filler-role representations. The initial sections on filler/role representations and analogies are not essential to the main experiments, so you can safely skip ahead to the main experiments if you wish.
Filler-role representations
Suppose you want to represent the abstract numerical quantity "the number of hours in a leap year." The standard way of writing this number is 8,784, which can be viewed as a filler-role representation that uses digits as fillers and powers of 10 as roles:
eight : thousands + seven : hundreds + eight : tens + four : ones
When we describe this number in words, the roles are actually made explicit. That is, the phrase "eight thousand seven hundred eighty-four" transparently corresponds to:
eight : thousand + seven : hundred + eight : ty + four : ∅
The only minor complications are the fact that the "-ty" suffix in "eighty" corresponds to the "tens" role and the fact that there is no pronounced instantiation of the "ones" role corresponding to the filler "four" at the end of the number.
With digits, the fact that positions are used as a shorthand for roles means that the order of the digits matters; the two copies of "8" in "8,784" mean different things (eight thousand vs. eighty). However, when using explicit filler-role pairs as in word representations, order no longer matters (this is partly why we have been using the + sign for linking together filler-role pairs, since order also does not matter for addition). Thus, even though Malagasy (the national language of Madagascar) uses a word order opposite that of English, it is still using fundamentally the same filler-role scheme (for clarity, hyphens have been added to the Malagasy words):
| Malagasy: | efatra | amby | valo- | folo | sy | fiton- | jato | sy | valo | arivo |
| English: | four | and | eight- | ty | and | seven- | hundred | and | eight | thousand |
| Fillers and roles: | four : ∅ + eight : ty + seven : hundred + eight : thousand | |||||||||
Filler-role representations are very flexible. There are many possible schemes for organizing the fillers, and many possible schemes for organizing the roles. For example, English standardly refers to the number 87 as “eighty-seven”, which uses powers of ten as roles:
87 = eight : tens + seven : ones
However, Abraham Lincoln used a different role scheme based on twenties, instead of tens, when he referred to 87 as “four score and seven” in the Gettysburg Address:
87 = four : twenties + seven : ones
It is also possible to alter the set of fillers. English standardly uses the digit words from “one” to “nine” as its fillers (with the absence of a filler being interpreted as the “zero”). However, in The Lord of the Rings, Bilbo Baggins refers to his age of 111 as "eleventy-one", a usage which expands the standard filler set to also include eleven:
111 = eleven : tens + one : ones
To give some more serious examples: Using bases besides 10 requires altering both the fillers and roles (e.g. base 7 uses only the fillers from 0 through 6, and its roles correspond to the decimal numbers 1, 7, 49, 343, etc.). Roman numerals also involve a complex set of fillers and roles that are difficult to characterize concisely. Moving beyond numbers, various types of linguistic units can be couched in terms of fillers and roles. In phonology, syllables involve the roles of onset, nucleus, and coda (with phonemes as fillers). In semantics, a sentence’s meaning involves roles such as AGENT and PATIENT, which are matched to specific entities as their fillers. Meanwhile, in syntax, noun-phrase fillers are associated with sentence-position roles such as subject and direct object.
Analogies
One popular method for investigating vector representations is through the use of analogies, which can be expressed as equations relating vectors to each other. For example, the analogy “king is to queen as man is to woman” can be expressed as:
king - queen = man - woman
Mikolov et al. (2014) found that this analogy does (approximately) hold for the word representations learned by word2vec. That is, the vector representing king minus the vector representing queen is approximately equal to the vector representing man minus the vector representing woman.
Such analogies are compatible with filler role representations. Suppose that we decompose the meanings of the words king, queen, man, and woman as follows:
king = royal : status + male : gender
queen = royal : status + female : gender
man = commoner : status + male : gender
woman = commoner : status + female : gender
Using these representations, we get:
king - queen = ( royal : status + male : gender ) - ( royal : status + female : gender )
man - woman = ( commoner : status + male : gender ) - ( commoner : status + female : gender )
Both of these equations reduce to male : gender - female : gender , meaning that the equation king - queen = man - woman is expected to hold under this representation of word meaning. Thus, this filler-role representation provides a possible explanation for why the analogy holds.
We can similarly use analogies to investigate whether the representations learned by our copying RNN are filler-role representations. This RNN is copying sequences such as 4,3,2,1,6. We will assume that the fillers it would use are the digits in the sequence, but there are multiple possible ways that it could represent the roles. For example, it could use positions counting from left to right, or positions counting from right to left, or a bidirectional role scheme that incorporates both directions:
4 , 3 , 7 , 9 = 4 : first + 3 : second + 7 : third + 9 : fourth
4 , 3 , 7 , 9 , 6 = 4 : fourth-to-last + 3 : third-to-last + 7 : second-to-last + 9 : last
4 , 3 , 7 , 9 , 6 = 4 : (first, fourth-to-last) + 3 : (second, third-to-last) + 7 : (third, second-to-last) + 9 : (fourth, last)
Certain analogies will only work for some role schemes but not others. For example, the following analogy works with left-to-right roles because both sides reduce to 2 : third . However, it does not hold with right-to-left roles or bidirectional roles because in those cases it does not reduce in any clean way:
4,6,2 - 4,6 = 3,9,2 - 3,9
On the other hand, the next analogy works with right-to-left roles (because both sides reduce to 4 : third-to-last ) but not for left-to-right roles or bidirectional roles:
4,6,2 - 6,2 = 4,3,9 - 3,9
This distinction can also be seen with whole numbers vs. numbers written after a decimal. Whole numbers use a right-to-left arrangement of digits, so the equation 462 - 62 = 439 - 39 is true. On the other hand, numbers after a decimal use a left-to-right arrangement of digits, so .462 - .62 = .439 - .39 is false, while it is true that .462 - .46 = .392 - .39.
Below, you can try different analogies using the vector representations generated by our copying RNN. This works by providing three sequences as three of the four elements of an analogy. The vector encodings of these three sequences are then used to determine the expected vector encoding of the fourth sequence. This expected encoding is then decoded using the decoder, and you can see whether the decoder produces the correct sequence to complete the analogy.
You can click "Generate left-to-right analogy" or "Generate right-to-left analogy" to automatically fill in analogies consistent with just one role scheme. The "Generate bidirectional analogy" button will automatically fill in an analogy that is consistent with any of these role schemes (left-to-right, right-to-left, or bidirectional). Alternately, you can click "Generate ambiguous analogies" to create an input set for which left-to-right and right-to-left role schemes would predict different answers, so that you can differentiate the two role schemes by seeing which of the two answers it does generate. Finally, you can manually type in sequences to create your own analogies.
| Left-to-right prediction: | N/A |
| Right-to-left prediction: | N/A |
| Decoder's output: | N/A |
The most salient points to notice from these analogies are the following:
- The right-to-left analogies almost never succeed.
- The left-to-right analogies usually succeed.
- The bidirectional analogies always succeed.
- On ambiguous analogies, usually the decoder's output either matches the left-to-right prediction, or neither prediction.
The fact that the bidirectional analogies always succeed while neither unidirectional analogy succeeds as reliably provides evidence that this model is using a filler-role representation with bidirectional roles. However, the fact that left-to-right roles are more successful than right-to-left roles suggests that, within the model's bidirectional role scheme, the left-to-right direction is weighted more heavily than the right-to-left direction.
These analogies offer some preliminary evidence that this neural network's representations are some sort of filler-role representation and that it uses a bidirectional role scheme. In the next section, we seek to investigate this hypothesis in a more comprehensive manner with a novel analysis tool, the Tensor Product Decomposition Network (TPDN).
Tensor Product Decomposition Networks
For a neural network to be implementing a filler-role representation, it must have some method for using a single, continuously-valued vector to represent the fillers and roles. We hypothesize that neural networks will accomplish this using Tensor Product Representations, which Smolensky (1990) introduced as a principled method for converting filler-role representations into vectors. Our implementation of Tensor Product Representations (which is a slightly modified version of the formulation in Smolensky (1990)) works as follows:

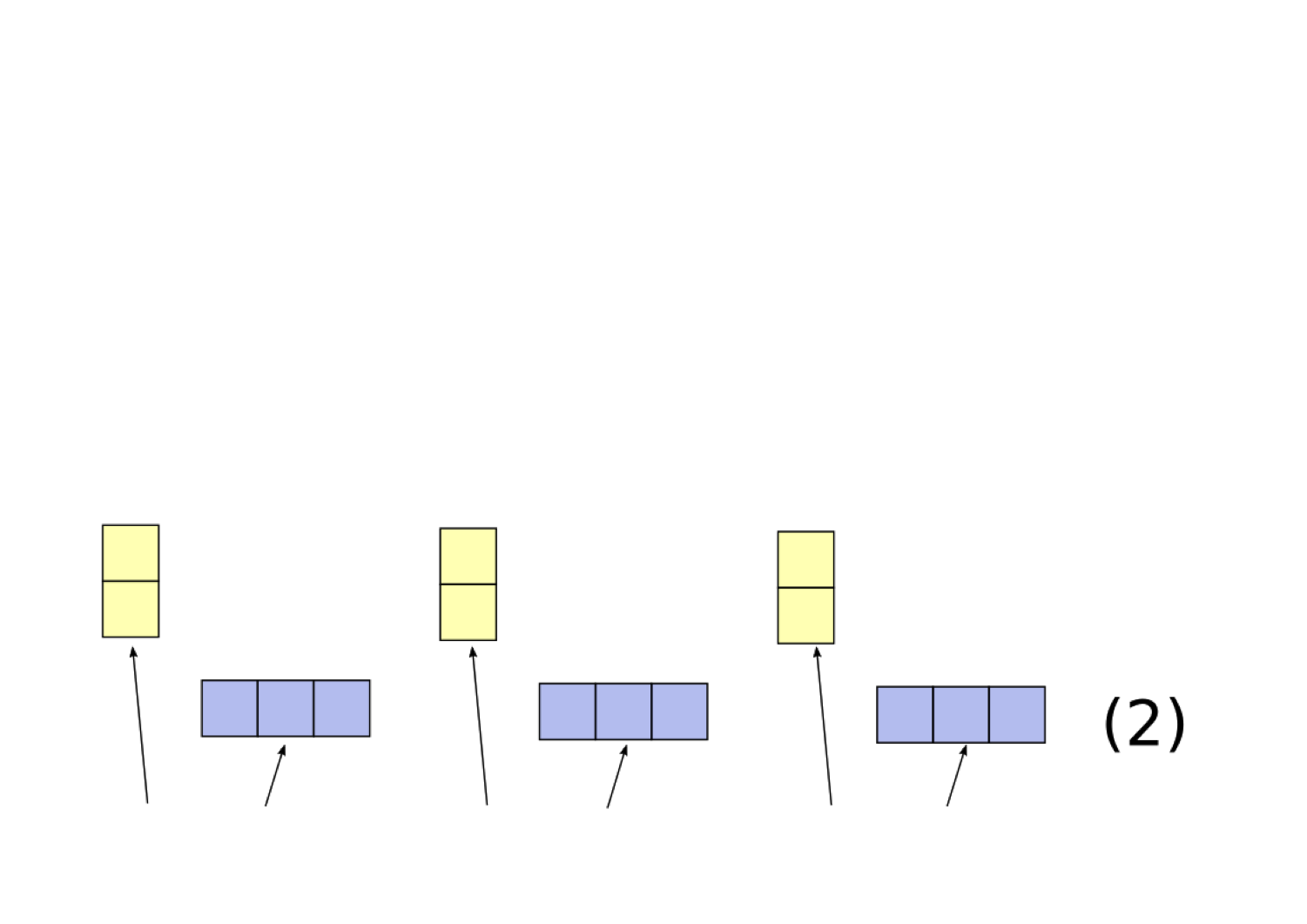
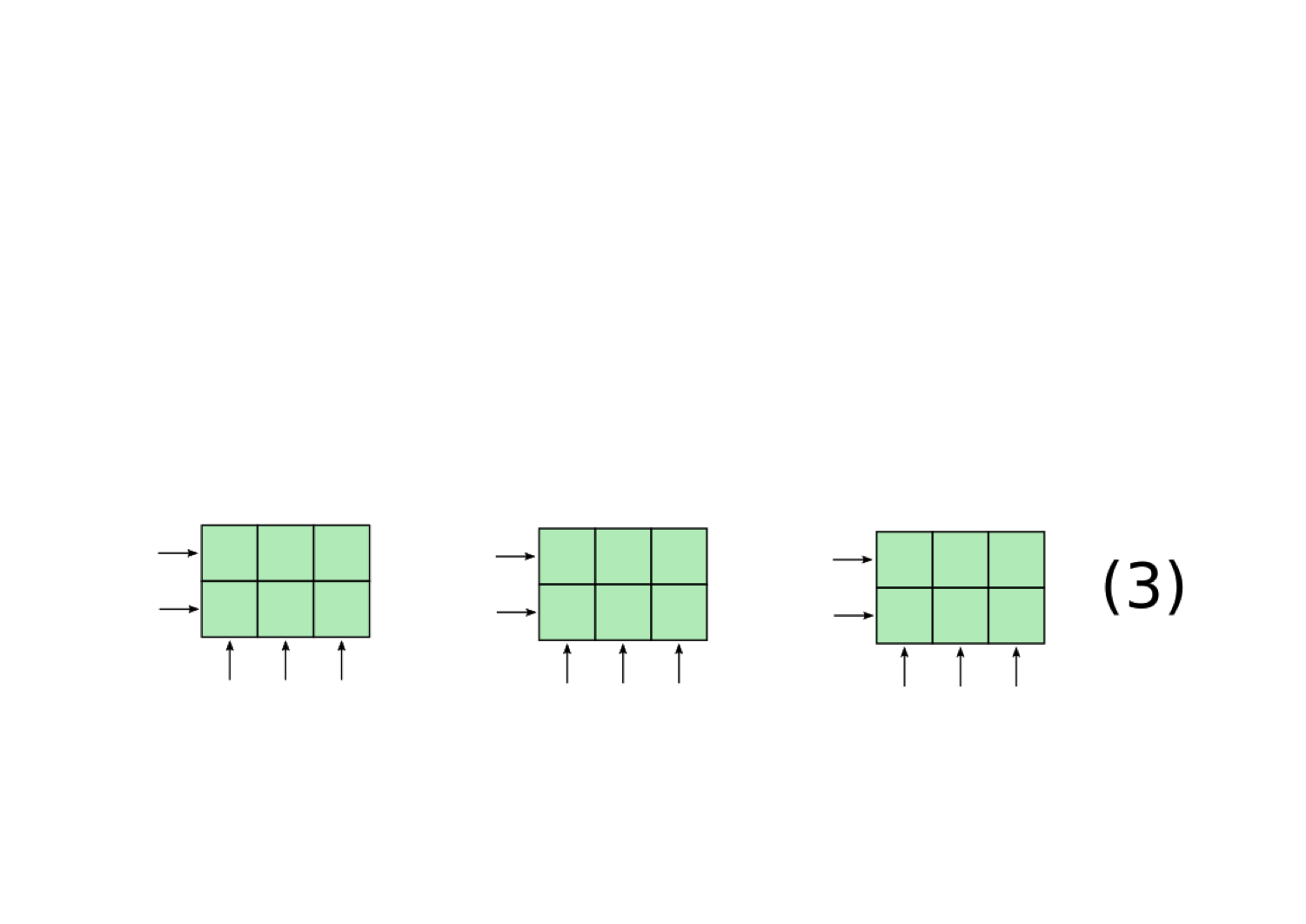
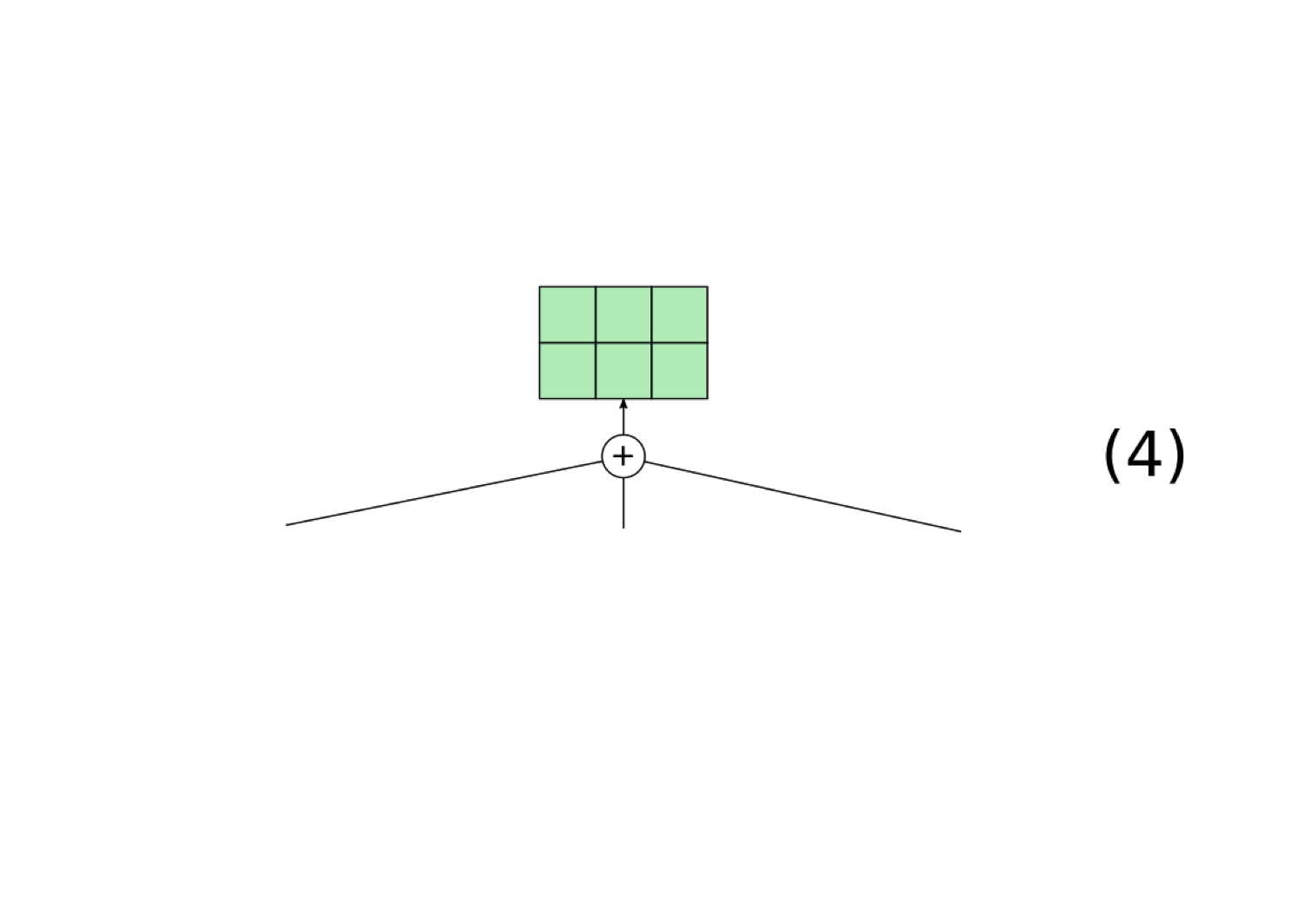
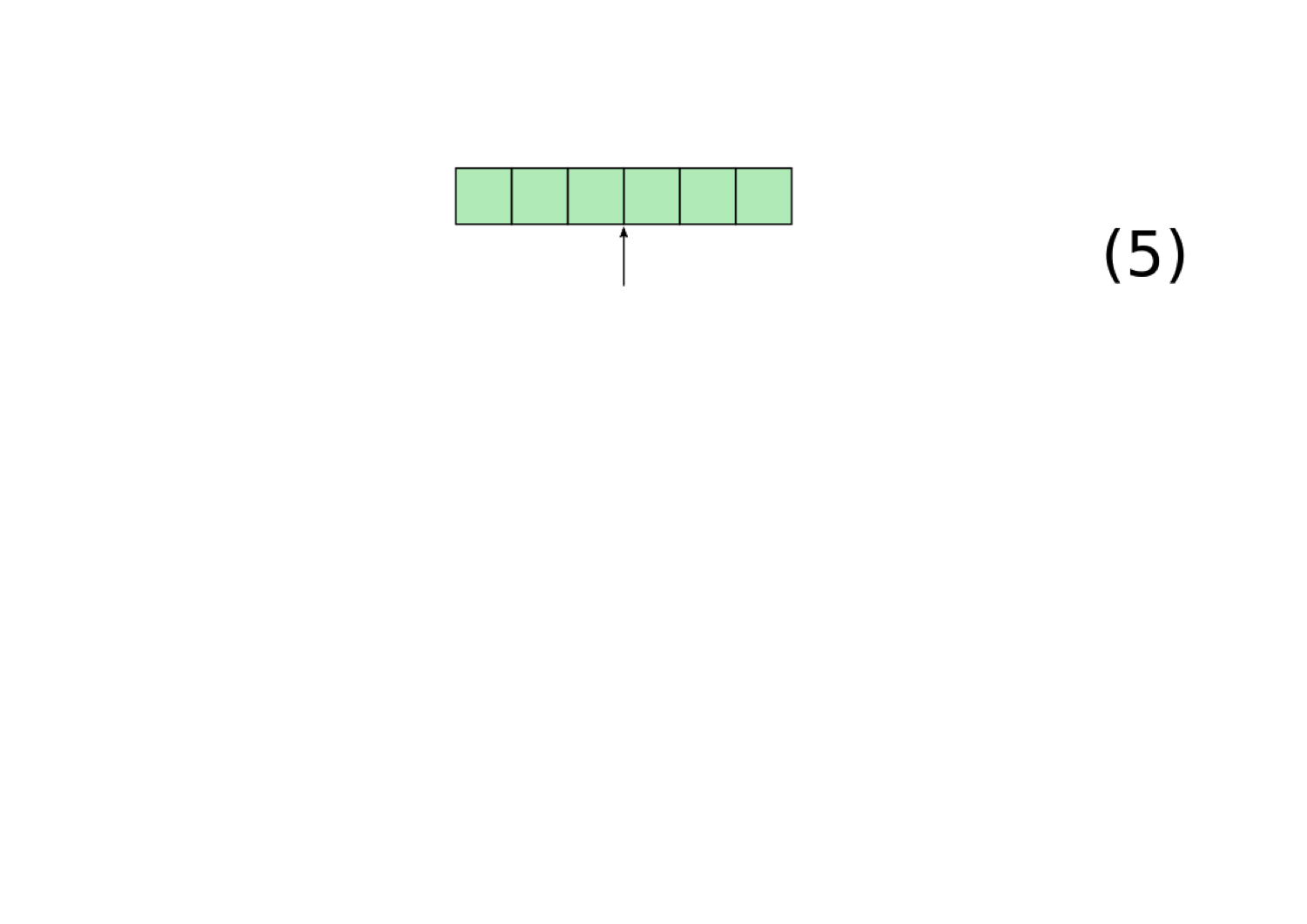
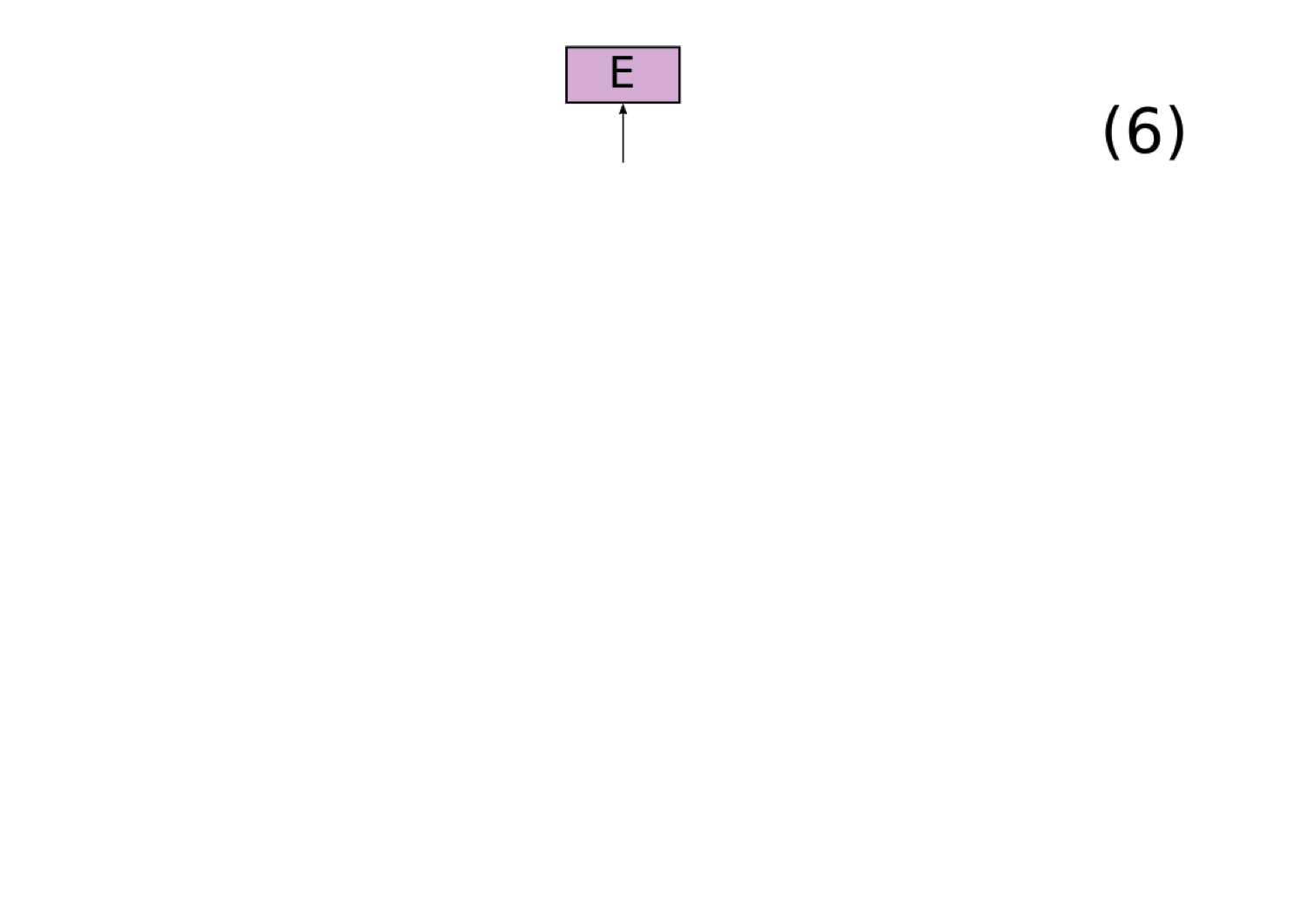
There is nothing in the structure of a neural network that restricts it to create a Tensor Product Representation. Nonetheless, Tensor Product Representations are a powerful technique for representing compositional structure in continuous space, which is why we hypothesize that neural networks may implicitly implement this formalism when they need to represent compositional structure.
To test whether our RNN's representations can be viewed as an example of a Tensor Product Representation, we introduce a novel architecture called the Tensor Product Decomposition Network (TPDN), which attempts to fit a Tensor Product Representation onto a set of vector representations such that the vector encodings produced by the TPDN are as close as possible to the vector encodings produced by the RNN.
Finding good role models
As input, the TPDN requires that the sequence be represented as a set of filler/role pairs. We assume that the digits in the sequence are the fillers, but there are multiple plausible techniques for assigning fillers to these roles. We investigate six possible role schemes:
Left-to-right roles: Each filler's role is its index in the sequence, counting from left to right. |
Type a sequence:
|
|
Right-to-left roles: Each filler's role is its index in the sequence, counting from left to right. |
Type a sequence:
|
|
Bidirectional roles: Each filler's role is an ordered pair containing its left-to-right index and its right-to-left index. |
Type a sequence:
|
|
Wickelroles: Each digit’s role is the digit before it and the digit after it. |
Type a sequence:
|
|
Tree positions: Each digit’s role is its position in a tree, such as RRL (left child of right child of right child of root). The tree structures are determined by an algorithm that clusters digits based on their values. |
Type a sequence:
|
|
Bag-of-words: All digits have the same role. We call this a bag-of-words because it represents which digits (“words”) are present and in what quantities, but ignores their positions. |
Type a sequence:
|
TPDN results
We evaluate the TPDN by seeing whether the RNN's decoder—which was trained on the encodings produced by the RNN encoder, not the encodings produced by the TPDN—can successfully produce the correct output sequence when fed an encoding from the TPDN. If it can, that is evidence that the TPDN is indeed providing a close approximation of the RNN encoder.
For each of the six role schemes above, we fitted a TPDN using that role scheme onto our copying RNN. You can test out these TPDNs in the following cell, which allows you to visually compare the vector encodings produced by the TPDN to the vector encodings produced by the RNN encoder, as well as to see if the RNN decoder can successfully decode from the TPDN's encoding:

The following chart gives the overall results. The bag-of-words bar cannot be seen because its value is essentially zero:
The differences between role schemes may be hard to discern when only looking at the vectors (though upon closer inspection differences can be found). However, looking at the output sequences or the results in the chart reveals the differences more clearly. Some of the most salient points from the chart and the simulation are:
- Bidirectional roles provide an extremely strong approximation of the RNN. Thus, the representations of this RNN can be apprximated strikingly well with a Tensor Product Representation.
- The left-to-right unidirectional roles also provide a good, but not quite as strong, approximation.
- Meanwhile, the right-to-left unidirectional roles perform poorly.
This asymmetry suggests that the model is implementing what we call mildly bidirectional roles: the representations are bidirectional in nature, but within this bidirectional role scheme the left-to-right direction is favored over the right-to-left direction. This conclusion is in line with the observations made about the analogies above.
The fact that this copying RNN appears to be implementing bidirectional roles provides a possible explanation for why it struggles with copying single-digit sequences. If a sequence is only a single digit long, then the bidirectional role scheme will assign that digit the role (1,1). However, this role occurs very rarely in the training set, since there are so few single digits; therefore, the RNN struggles with sequences involving this role.
Effect of training task
We can use the TPDN to delve deeper into different aspects of RNN training to see how those aspects affect the representations that are learned. First, we can see how the training task affects the representations. So far we've focused on one task (copying, aka autoencoding), but now we expand the set of tasks to include three others:
The following chart displays how the training task affects the learned representation (this chart also allows you to vary the architecture being considered. See the next section for descriptions of the architectures):
There are several points to note about this graphic (all focusing on the unidirectional/unidirectional architecture):
- As noted above, on the autoencoding task, the model appears to learn bidirectional roles that strongly favor the left-to-right direction over the right-to-left direction.
- By contrast, on the reversal task, the model learns right-to-left roles, with left-to-right roles performing poorly. This makes sense given the backwards relationship between copying and reversal.
- For the interleaving task, the model still learns bidirectional roles, but now neither single-direction role scheme (whether left-to-right or right-to-left) works well on its own. This makes sense given that interleaving heavily depends on representations of indices in both directions.
- For the sorting task, all role schemes perform strongly. Most notably, the bag-of-words role scheme (which is essentially the absence of structure) performs just as well as the other role schemes, whereas it fails miserably in the other three tasks. This suggests that, for the sorting task, the model learns to ignore all sequence structure (since that structure is irrelevant for the sorting task).
- In many cases, these results show high accuracies for more than one role scheme. This happens because some role schemes can be viewed as degenerate cases of other role schemes. For example, on the sorting task, all role schemes perform well. We interpret this fact to mean that the sorting models use bag-of-words roles because, if a seq2seq model can be approximated with bag-of-words roles, it is also possible to approximate it with any other role scheme by simply making all of the role embedding vectors the same (thereby making that role scheme functionally equivalent to a bag-of-words role scheme). Similarly, high accuracy with both right-to-left and bidirectional roles is indicative of right-to-left roles (since right-to-left roles are a degenerate case of bidirectional roles, meaning that a model that can be approximated well with right-to-left roles can also be approximated equally well with bidirectional roles). Therefore, we would only conclude that a model is actually using bidirectional roles if we observe high accuracy with the bidirectional role scheme and low accuracy with all other role schemes, which is what happens with the interleaving task.
Effect of architecture
Finally, we also investigate how the model architecture affects the learned representations. We investigate three model topologies: unidirectional, bidirectional, and tree-based. Each topology can be used for the encoder and/or the decoder. The following graphic shows, for a given task, how the encoder and decoder affect the learned representations. Each architecture is denoted as encoder/decoder (e.g., "Bi/Tree" means a model with a bidirectional encoder and a tree-based decoder):
There are two major things to notice from these graphics:
- The model architecture does affect the learned representations. For example, on the autoencoding task, the unidirectional/unidirectional model is approximated very well with bidirectional roles, while the tree/tree model is approximated very well with tree position roles.
- The decoder largely dictates the representation, while the encoder has little effect. This can be seen from the fact that, within a row (i.e. when the decoder is varied with a fixed encoder), the results vary significantly; while within a column (i.e. when the encoder is varied with a fixed decoder), the results vary little.
Conclusions: Making the black box a little grayer
Analysis using TPDNs shows that neural networks can learn to use structured, compositional representations to solve symbolic tasks. However, just because they can generate such representations does not mean that they always do. The results described here all deal with heavily structure-dependent tasks operating over sequences of digits. When we extend the results to sentence representations based on corpora of naturally-occurring text, the TPDN analysis suggests that popular sentence-encoding models generally lack any sort of robust, systematic structure (see the full paper for more details). This finding is in line with what we observed on the models trained to perform sorting: Because this task does not depend on structure, the models trained to perform this task learned to discard most structural information in the input, with the result that these models' representations could be well-approximated with bag-of-words roles.
Therefore, we view our experiments on how the representation is affected by the architecture and the training task as a preliminary investigation of the situations under which neural networks will learn structured, compositional representations. Our results indicate the importance of the architecture (particularly the decoder) as well as the training task in determining the types of representations a model will learn. Extending such work may provide insight for improving current neural models to make them less brittle and better able to generalize to novel domains.
Questions? Comments? Email tom.mccoy@jhu.edu.
