Uncovering the implicit filler-role structures in RNNs

This page accompanies the paper found here. The code is available here.

Introduction

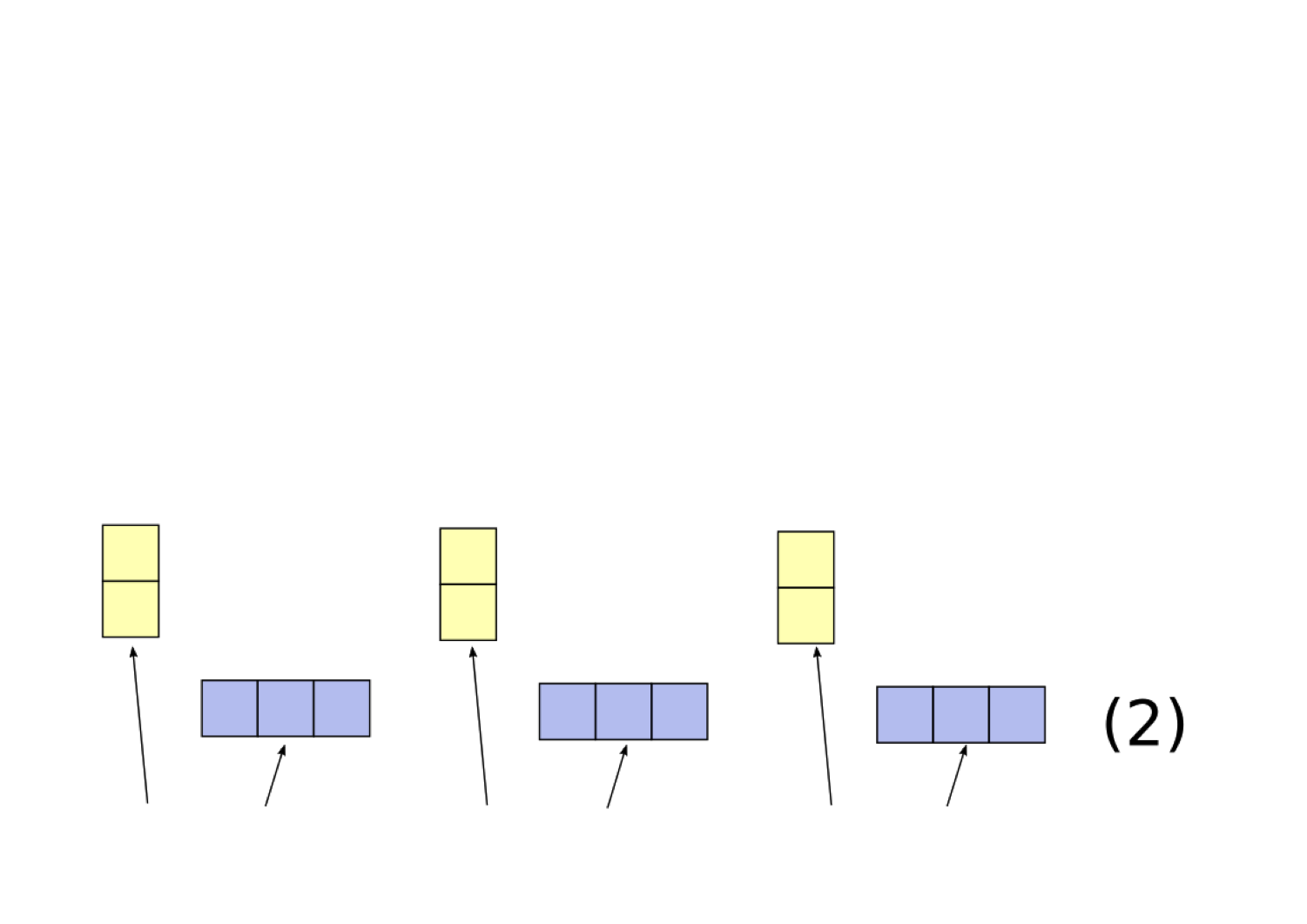
In order to carry out symbolic tasks, it intuitively seems necessary to have discrete, symbolic representations. For example, consider the task of copying a list of digits. To do this, it seems necessary to represent the list in a way that identifies both its fillers—that is the elements of the list—and those filler's roles—that is their positions in the list.For example, a filler-role representation of the list 6,4,3,9,1 might be:

6:first + 4:second + 3:third + 9:fourth + 1:fifth

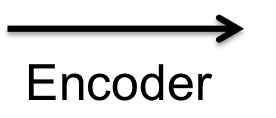
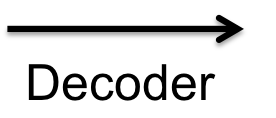
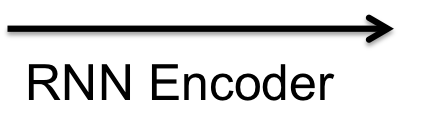
Neural networks do not appear to use such explicit representations of structure, yet they can still carry out symbolic tasks very successfully. For example, the following box contains a recurrent neural network (RNN) trained to perform the copying task. It has two components: the encoder, which encodes the sequence into a vector of continuous values (represented here as various shades of blue); and the decoder, which takes the vector encoding as input and uses it to generate the output sequence.

This network is not perfect—for example, it fails on most sequences that are only a single digit long—but it does perform extremely well, with over 99% accuracy on a held-out test set. The question, then, is how can neural networks use their continuous vector representations to perform tasks that seem to depend on discrete, symbolic structure?

We investigate the following hypothesis:

Hypothesis: Neural networks trained to perform symbolic tasks will implicitly implement filler/role representations.

Deeper evidence: TPRs

In order for our RNN to be implementing a filler/role representation, it must have some way for representing the fillers and roles within a continuous vector. We focus on an existing proposal for doing this called the tensor product representation (TPR; Smolensky 1990), which provides a principled way to represent filler/role representations in vector space. Our implementation of tensor product representations works as follows (this is a slightly modified version of the one from Smolensky 1990):

(1) Represent the sequence as pairs of fillers and roles.

(2) Embed each filler and each role.

(3) Bind the filler and role vectors using the tensor product.

(4) Sum the tensor products.

(5) Flatten the sum into a vector by concatenating its rows.

(6) Apply a linear transformation to the sum to generate the final encoding, E.

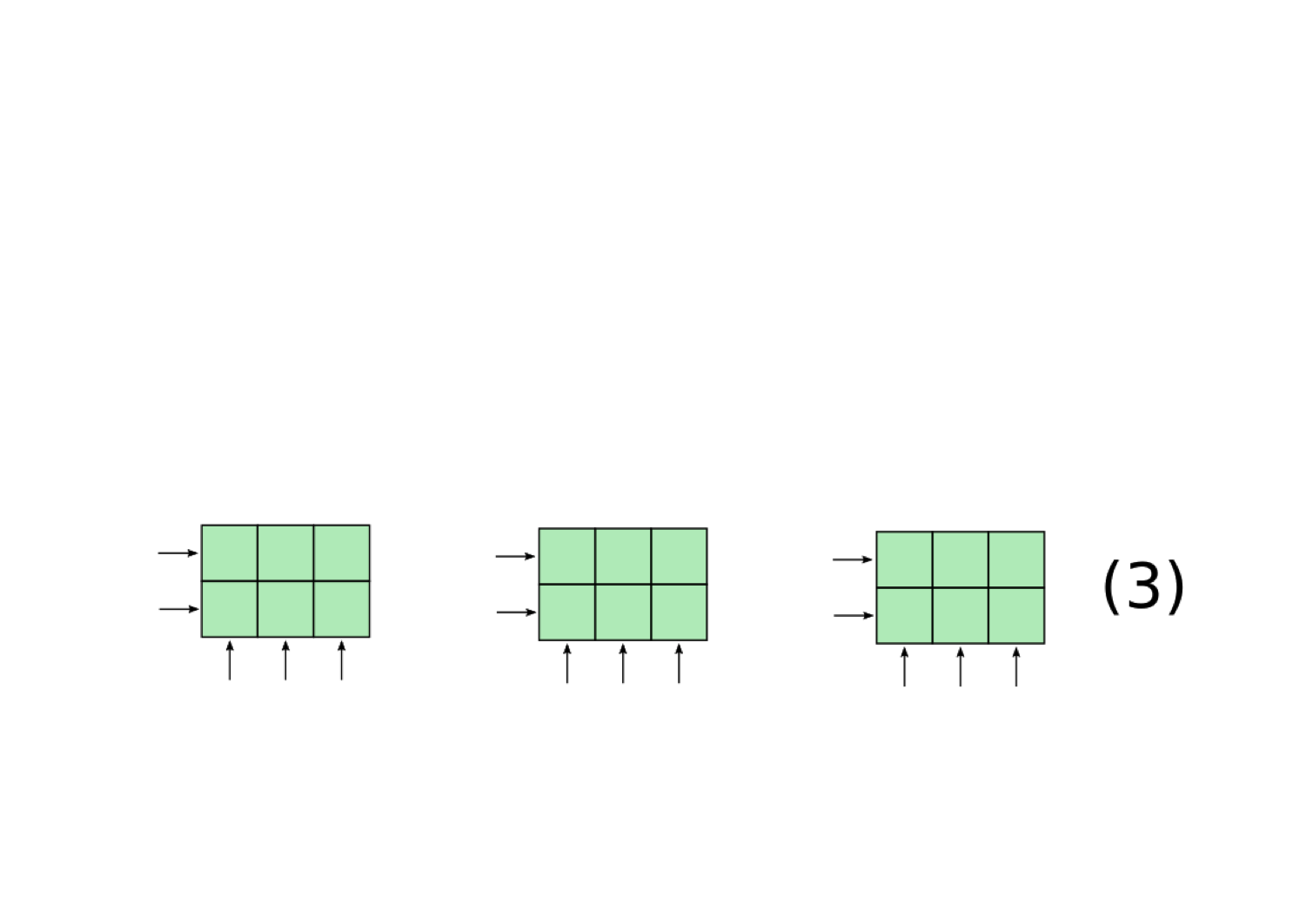
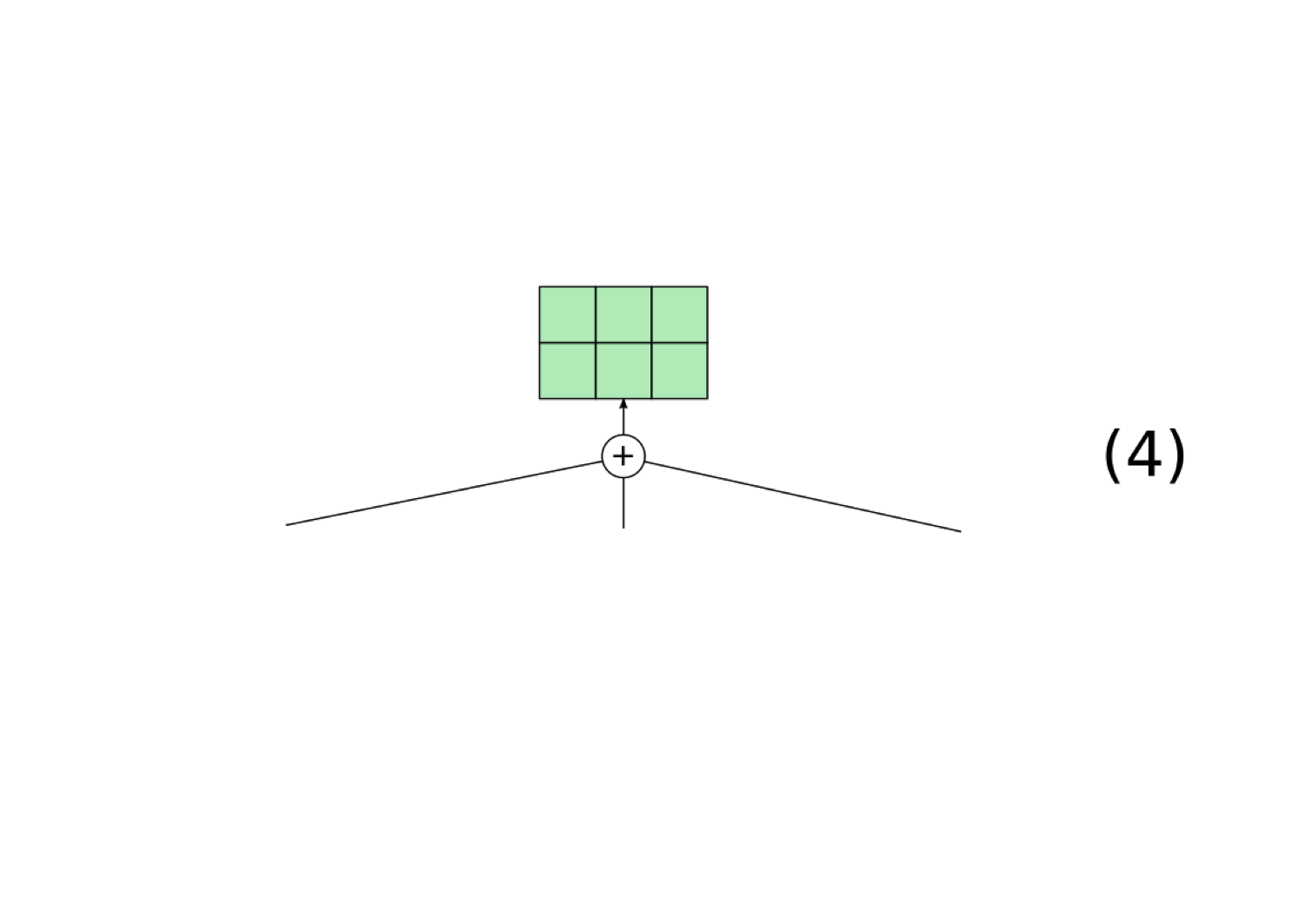
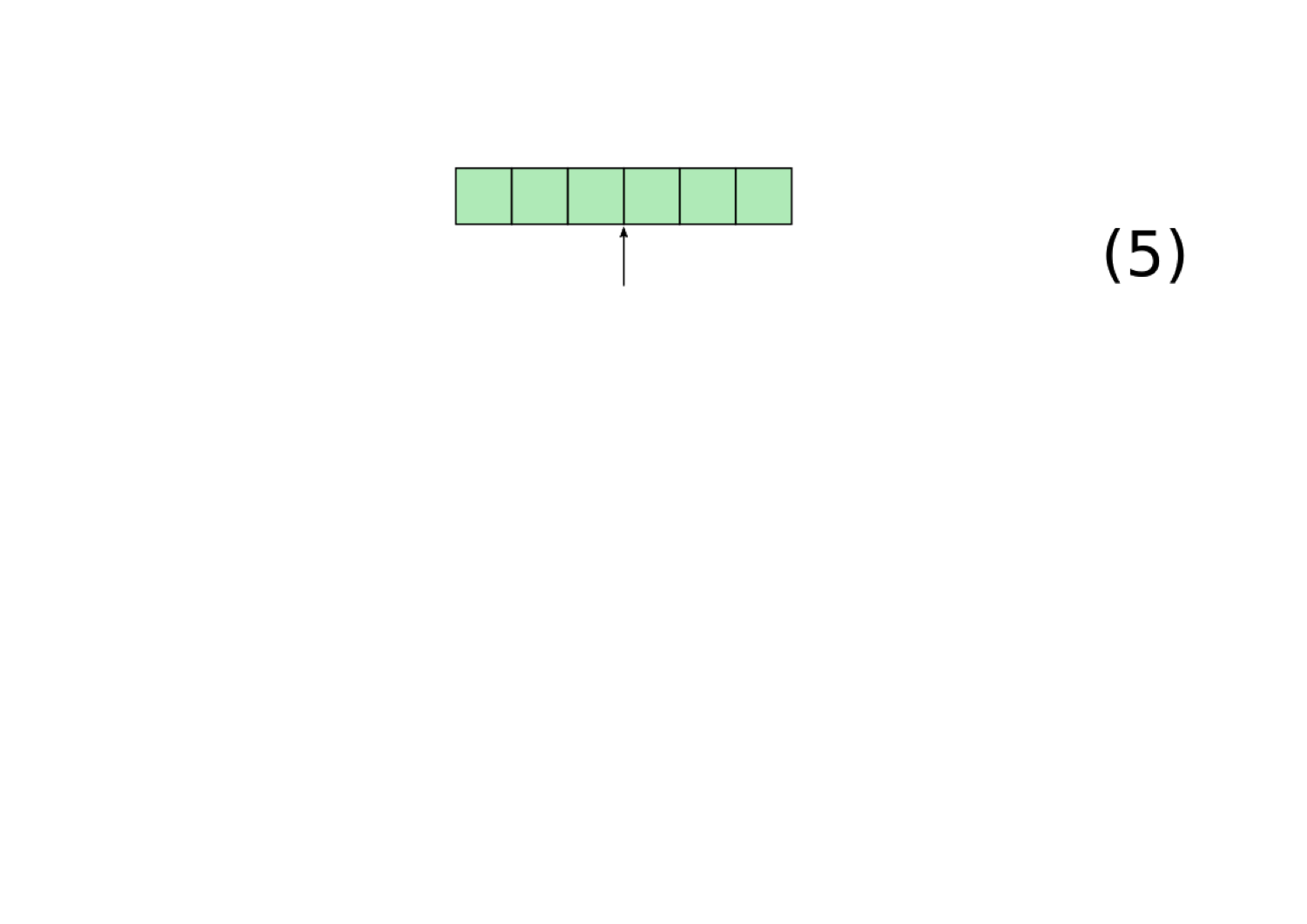
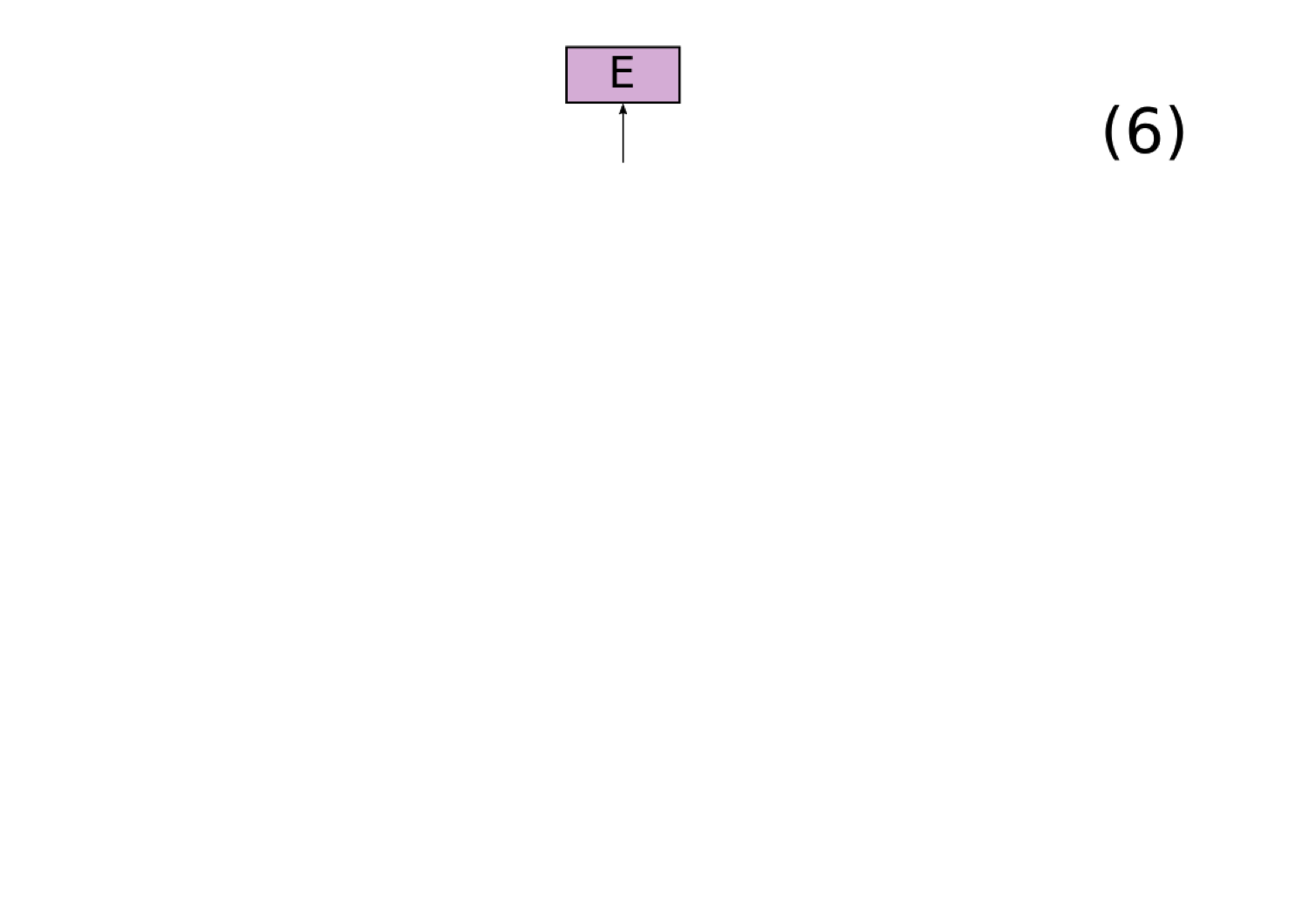
To test whether our RNN's representations can be viewed as an example of a TPR, we introduce a novel architecture called the Tensor Product Decomposition Network (TPDN), which attempts to fit a tensor product representation onto a set of vector representations such that the vector encodings produced by the TPDN are as close as possible to the vector encodings produced by the RNN.

For the TPDN to work, it needs to be provided with a scheme for assigning roles to fillers. Our examples so far have used indices counting from left to right as the roles, but there are other plausible ways of assigning roles as well. We investigate six different possible role schemes:

We evaluate the TPDN by seeing whether the RNN's decoder—which was trained on the encodings produced by the RNN encoder, not the encodings produced by the TPDN—can successfully produce the correct output sequence when fed an encoding from the TPDN. If it can, that is evidence that the TPDN is indeed providing a close approximation of the RNN encoder.

For each of the six role schemes above, we fitted a TPDN using that role scheme onto our copying RNN. You can test out these TPDNs in the following cell, which allows you to visually compare the vector encodings produced by the TPDN to the vector encodings produced by the RNN encoder, as well as to see if the RNN decoder can successfully decode from the TPDN's encoding:

The following table gives the overall results:

From this chart and the simulation, there are a few things to notice:

• Bidirectional roles provide an extremely strong approximation of the RNN.
• The left-to-right unidirectional roles also provide a good, but not quite as strong, approximation.
• Meanwhile, the right-to-left unidirectional roles perform poorly.

This asymmetry suggests that the model is implementing what we call mildly bidirectional roles: blah blah blah.

The fact that this copying RNN appears to be implementing bidirectional roles provides a possible explanation for why it struggles with copying single-digit sequences. If a sequence is only a single digit long, then the bidirectional role scheme will assign that digit the role (1,1). However, this role occurs very rarely in the training set, since there are so few single digits; therefore, the RNN struggles with sequences involving this role.

Further evidence: Analogies

We can preliminarily test this hypothesis by using analogies, which are a popular source of evidence for understanding vector representations. We will express these analogies as equations. For example, if the vector representations of our copying RNN use the filler-role representation discussed above, we would expect the following equation to hold (where an arrow over a sequence is used to denote the vector representation of the sequence):

6,8,2,7 - 6,3,2,7 = 4,8,0,5,1 - 4,3,0,5,1

We expect this to hold because, if we expand each sequence out into a filler/role representation, the two sides of the equation both reduce to 8:second - 3:second, so the equation would be true:

(6:first + 8:second + 2:third + 7:fourth) - (6:first + 3:second + 2:third + 7:fourth) = (4:first + 8:second + 0:third + 5:fourth + 1:fifth) - (4:first + 3:second + 0:third + 5:fourth + 1:fifth)

So far we have been assuming that the roles are each digit's index counting from left to right. However, there are many other valid ways of assigning roles to fillers, such as instead using indices counted from right to left. With this right-to-left role scheme, the same analogy from above no longer holds because the equation now reduces to 8:third - 3:third = 8:fourth - 3:fourth, which is not necessarily true:

(6:fourth + 8:third + 2:second + 7:first) - (6:fourth + 3:third + 2:second + 7:first) = (4:fifth + 8:fourth + 0:third + 5:second + 1:first) - (4:fifth + 3:fourth + 0:third + 5:second + 1:first)

Motivated by the fact that certain analogies work for certain role schemes but not others, we can test whether the RNN representations from above are consistent with specific role schemes by looking at analogies catering to each role scheme. We test six different role schemes:

These analogies provide independent evidence for the conclusions of the TPDN analysis, namely that...

Effect of training task

We can use the TPDN to delve deeper into different aspects of RNN training to see how those aspects affect the representations that are learned. First, we can see how the training task affects the representations. So far we've focused on one task (copying, aka autoencoding), but now we introduce 3 more symbolic tasks:

The following chart displays how the training task affects the learned representation (this chart also allows you to vary the architecture being considered. See the next section for descriptions of the architectures):

There are several points to note about this graphic (all focusing on the unidirectional/unidirectional architecture):

• As noted above, on the autoencoding task, the model appears to learn bidirectional roles that strongly favor the left-to-right direction over the right-to-left direction.
• By contrast, on the reversal task, the model learns right-to-left roles, with left-to-right roles performing poorly. This makes sense given the backwards relationship between copying and reversal.
• For the interleaving task, the model still learns bidirectional roles, but now neither single-direction role scheme (whether left-to-right or right-to-left) works well on its own. This makes sense given that interleaving heavily depends on representations of indices in both directions.
• For the sorting task, all role schemes perform strongly. Most notably, the bag-of-words role scheme (which is essentially the absence of structure) performs just as well as the other role schemes, whereas it fails miserably in the other three tasks. This suggests that, for the sorting task, the model learns to ignore all sequence structure (since that structure is irrelevant for the sorting task).

Effect of architecture

Finally, we also investigate how the model architecture affects the learned representations. We investigate three model topologies: unidirectional (where...), bidirectional (where...), and tree-based (where...). Each topology can be used for the encoder and/or the decoder. The following graphic shows, for a given task, how the encoder and decoder affect the learned representations.

INSERT ARCHITECTURE GRAPHIC

There are two major things to notice from these graphics:

• The model architecture does affect the learned representations. For example, on the autoencoding task, the unidirectional/unidirectional model implements bidirectional roles, while the tree/tree model implements tree position roles.
• The decoder largely dictates the representation, while the encoder has little effect.

Conclusions

Blah blah blah.

It has long been held that compositional structures are necessary for performing symbolic tasks. However, neural networks are capable of carrying out such tasks despite the fact that they do not utilize any obvious compositional structure. For example, the following cell contains a recurrent neural network encoder/decoder that has been trained to perform the task of autoencoding (taking a sequence as input and returning the same sequence as output). It performs this task by first encoding the sequence, that is transforming it into a vector that represents the sequence. The decoder then decodes this vector to produce the output.

Intuitively, it seems that the autoencoding task requires some representation of which digits appear in the sequence and where they appear.

We hypothesize that

Tensor Product Decomposition Networks

Tensor Product Representations: Embedding structure in continuous space

Role schemes

The example above used linear indices (counting from left to right) to denote the roles of the elements of the sequence. However, there are other possible ways to do this instead.